II- Review of the Nature Principles (cont.)

e) Finiteness

Infinite, as perpetual growth, does not exist. Earth, as well Universe, is limited.

In the Nature, there is no permanent growth, that is to say, all which is born, has to die, or all which rises, has to come down again.

Suppose a bacteria doubling every 30 minutes. After one week all Solar System will be filled, and after 11 days all Universe will be filled.

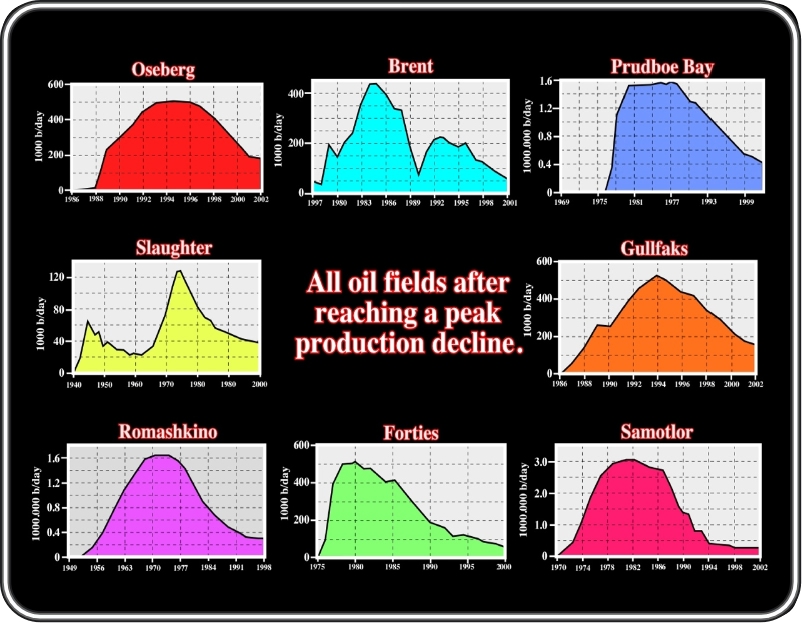
The rate of decline varies according to the volumes each field was producing when it peaked. Hydrocarbon output begins to decline as encroaching water and gas simply crowd out the oil (M. Simmons, 2005).

Three spaces are possible in relativity:

1) No curvature

2) Positive curvature

3) Negative curvature

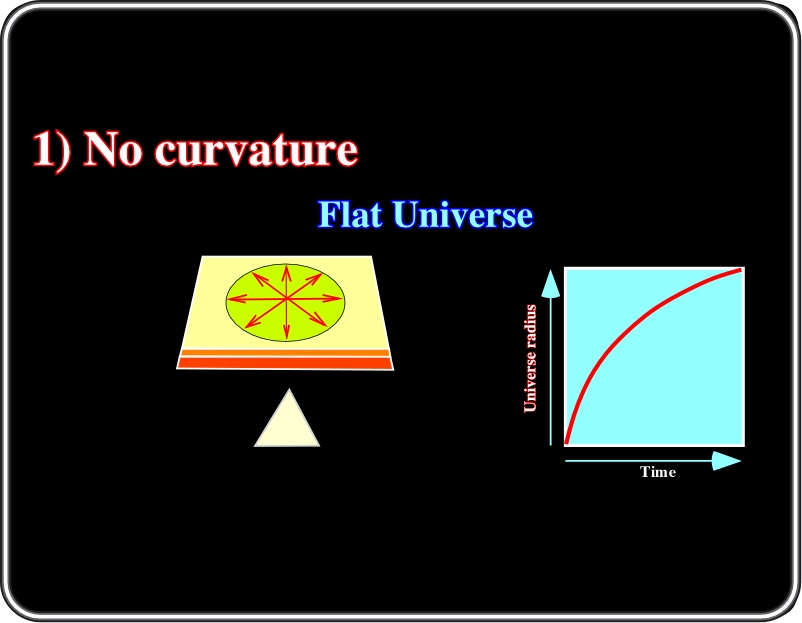
In a no curvature model, the radius of the Universe increases with time, but sooner or later the increasing becomes smaller and smaller.

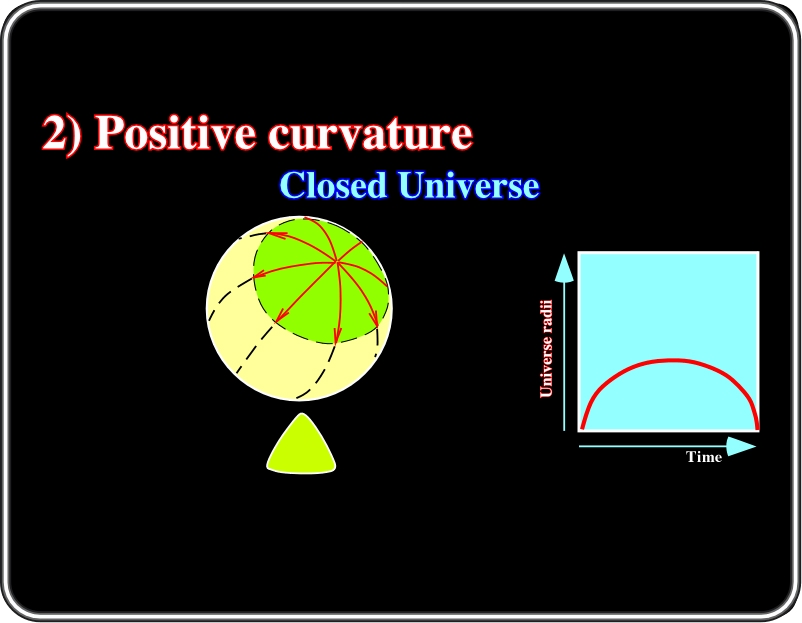
In a positive curvature model, the radius of the Universe increases with time, but after reaching a maximum it decreases progressively till a big crunch take place.

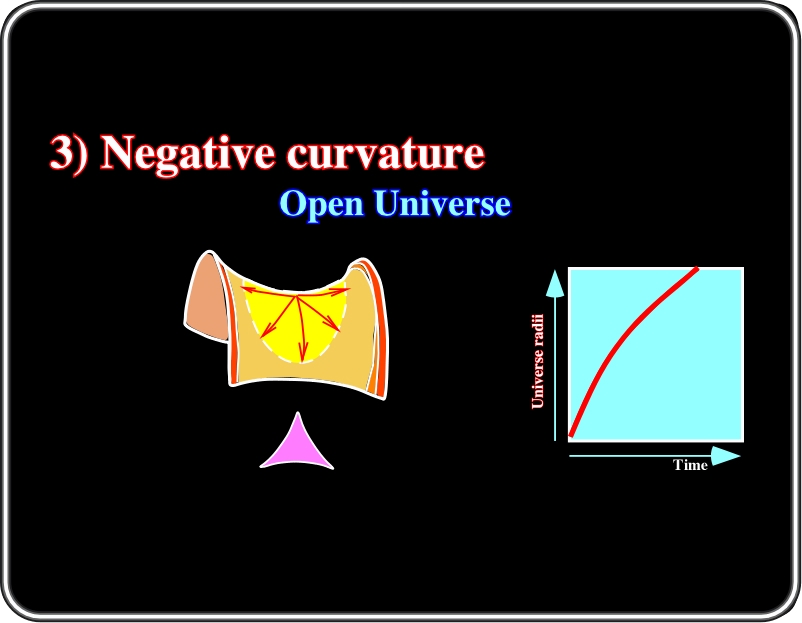
In a negative model, the radius of the Universe increases with time, that is to say, that there is nor enough material to counterbalance gravitation. The more likely, of all these models seems to be the one with a positive curvature (2).

What means finiteness in mathematical terms?

Suppose this natural distribution: 2, 4, 6, ?, ?, ? , with rank: 1,2,3,..........n-2, n-1, n and value: 2, 4, 6,........N-2, N-1, N. How many solutions do you propose?

There is a large number of solution: there are, at least 14 solutions (1st degree)

2, 4, 6, 8, 10, 12, 14, 16 N=2n or N=(N-1)+2
2, 4, 6, 10, 16, 26, 42, 68 N=(N-1)+(N-2)
2, 4, 6, 8, 10, 12, 14, 16 N=2(N-1)-(N-2)
2, 4, 6, 6, 0, -18, -54, -108 N=3(N-1)-3(N-2)
2, 4, 6, 4, -14, -76, -234, -556 N=4(N-1)- 9(N-2)

and so on

However, Occam’s razor suggests the simplest, i.e. minimum complexity:

2, 4, 6, 8, 10, 12, 14, 16 N=2n but

In Nature, too simple is often false:

All that is simple is false and all that is complex is useless.
(Paul Valéry)

Continuous growth is impossible in Nature

Indeed, the series 2, 4, 6, ?, ?, ?, has a beginning and grows, in life, it should peak and decline, in addition, negative values do not exist.

The simplest natural answer is 2,4,6,6.0 (N=3(N-1)-3 (N-2). Notice that modeling is just an approximation (there are no negative values in Nature). It should be simple and convenient. Many models can fit the data, but some give unrealistic extrapolations. Try different models and check the extrapolations. Select the models that fit other natural distributions.

The simplest natural answer is 2, 4, 6, 6, 0 N=3(N-1)- 3(N-2). Therefore, the same happens with oil production, remaining reserves, oil discoveries, etc.

These plate clearly indicated that since 1960 the oil discoveries are smaller and smaller. Indeed, any large oil field as Burgan, Zuata or Ghawar was found since the 60's. Indeed, it is quite evident that we are leaving from the past. Remember that since the 80s the majority of oil companies, and particularly the major, are enable to replace their production.

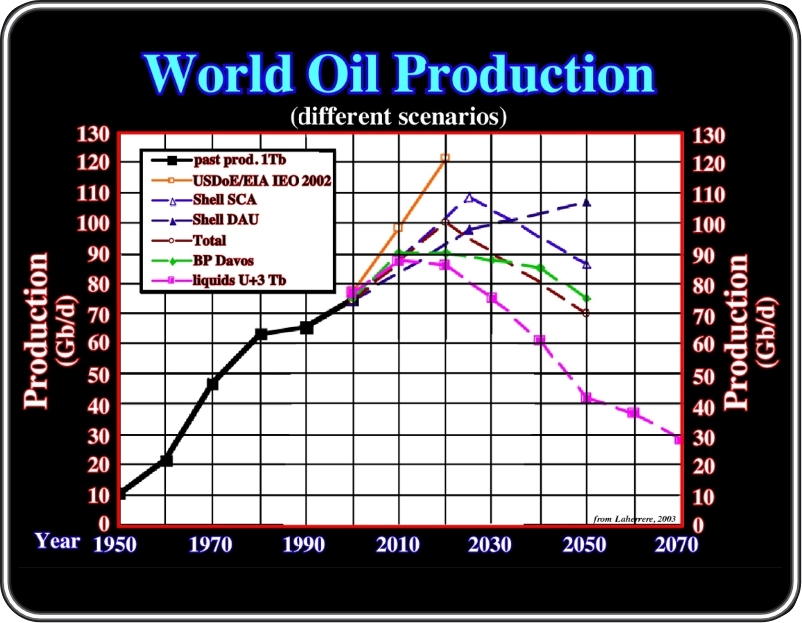
Assuming that when oil production peaks half of the reserves have already been produced, one can said that cheap oil is finished. Probably, very soon, if not already, we will be in left part of the purple curve. The discrepancies between the curves are artificial; lot of them are based in political and not technical data.

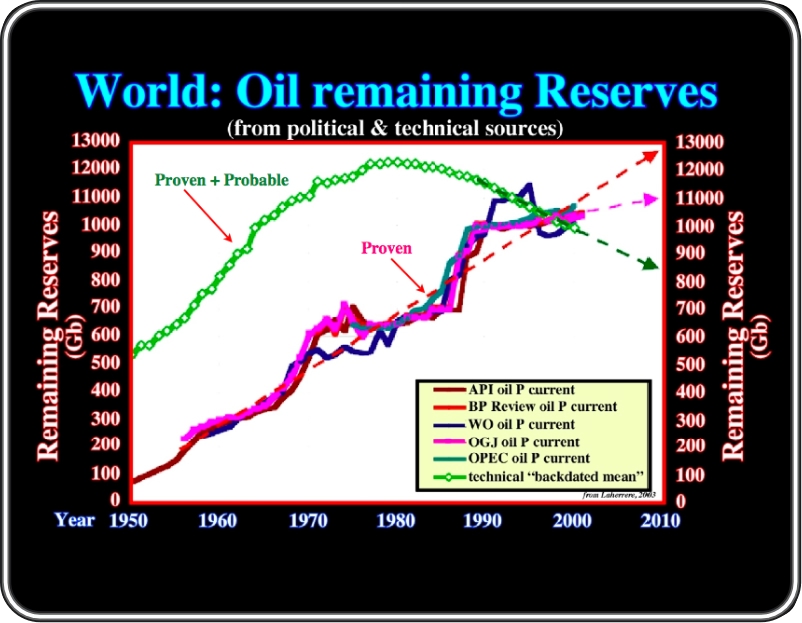
Those acquainted with oil business know reserves can changes according economical and political interests. On this plot, the green curve, made up with technical data (proven + probable, corrected), strongly indicated that since 1980, the oil produced is not replaced by discoveries. This obvious fact does not interest to several oil companies and government, which assume an eternal growth (proven) (”nihil aliud opus est”). USA companies follow the Securities and Exchange Commission which, contrariwise to the all other countries, publishes only proved reserves (financial data) and not probable reserves (technical data).

to continue press next