II- Review of the Nature Principles (cont.)

b) Self-Similarity

Nature is characterized by self-similarity. Natural objects have a fractal geometry.

Simulation of crystal growth. The fine structure of the “crystal” is self-similar. A part is similar to the whole. However, it is relevant here to point out that the sum of the part is not equal to the whole. The whole is more than the sum of the parts and its characteristics cannot be approached by the study of the parts in isolation.

A natural object, or geometric figure, is fractal when:

1) Its parts have the same shape (structure), in spite of their scale or deformation.

2) Its shape is either irregular, interrupted or fragmented independently the scale of observation.

3) It contains distinctive elements, which scales are very varied and covering a very wide range.

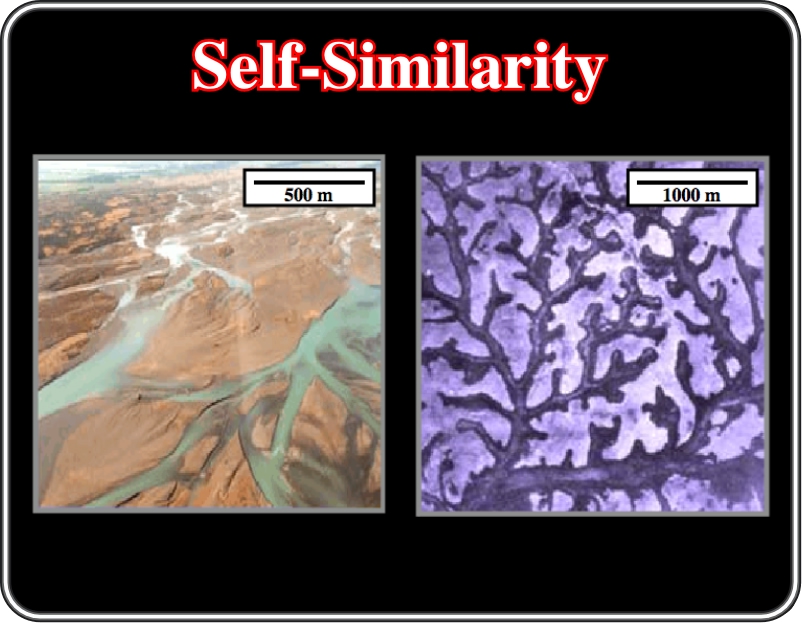
Braided streams and fluvial patterns have a fractal geometry: a part is similar to the whole.

Fractal dimension is a number that quantify the degree of irregularity and fragmentation of a geometric set or a natural object and which is reduced, in the case of the objects of the Euclid's usual geometry, in their usual dimensions (point, D=0; line, D=1; plane, D=2; cube, D=3).

On this line of Gulf of Mexico, in turbidite depositional systems, self-similarity is paramount. Indeed, in slope fans, channel-levees complexes (whole) are composed by a multitude of parts with same shape and structure in spite of their small scales.

Fractal concepts are clearly predominant in the study of dynamic systems behavior and dissipative systems (SOCs).

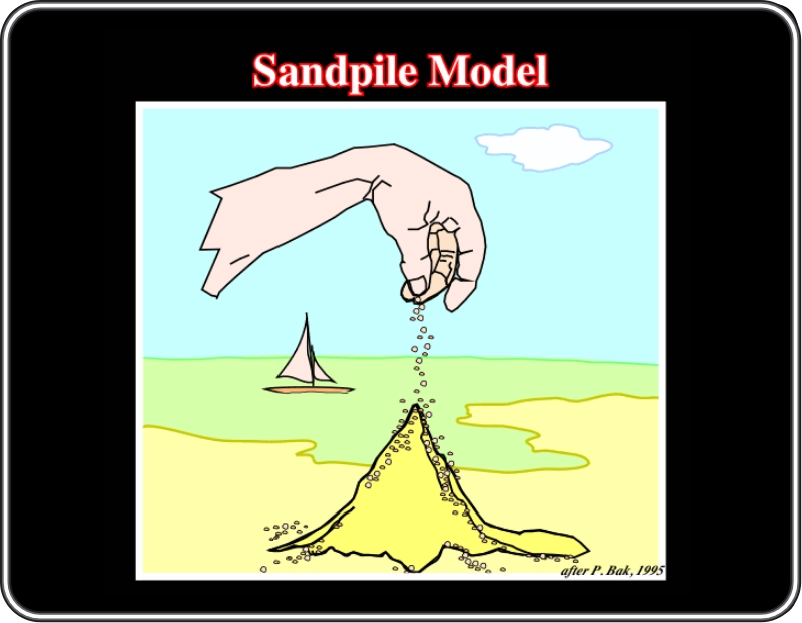
The sandpile is the canonical example of a Self-Organized Critical system (SOC). It exhibits a punctuated equilibrium behavior, where periods of stasis are interrupted by intermittent sand slides (as in turbidite systems). It can be expressed as a straight line on a double logarithmic plot, which indicates that the number of events is given by a simple power law: N(s) = s-π. The exponent π is defined as the slope of the curve. Catastrophic events, fractals, 1/f noise (fractals in time), Zipf’s law, etc., are examples of SOCs. They evolved to complex critical state without interference from any outside agent.

Geoscientists know a scale is necessary to interpret an outcrop or seismic line. Geology is scale dependent.

Without scales, orientation and location (outside of the geological setting) and the geological interpretation of a seismic line is meaningless, because self-similarity. Indeed, a slope delta is similar to a continental slope and to any offlap.

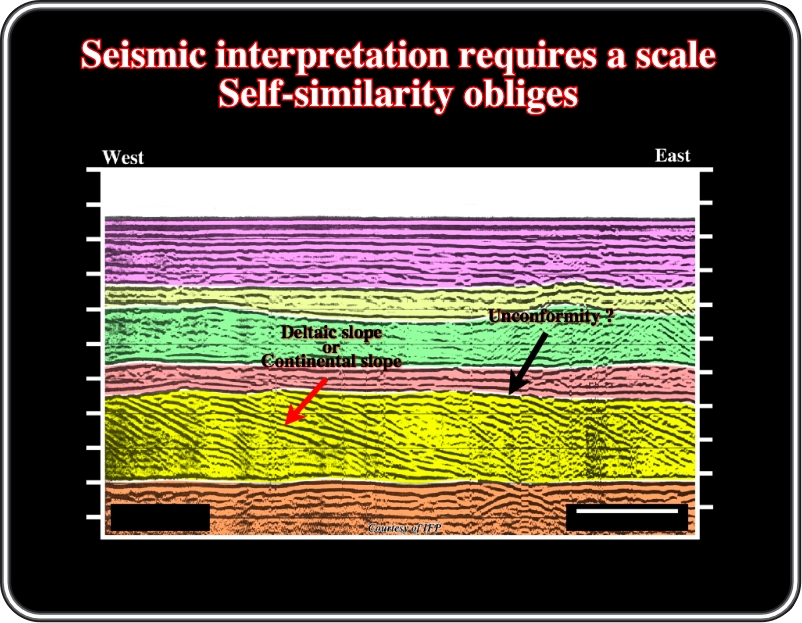
As Geology is scale dependent, geological seismic interpretations cannot be performed without knowing the scales, as well as the global and regional settings. On this line, interpreters will be enable to interpret the depositional inclined reflector. The reader is supposed to make a guess: shelf or slope downlaps?

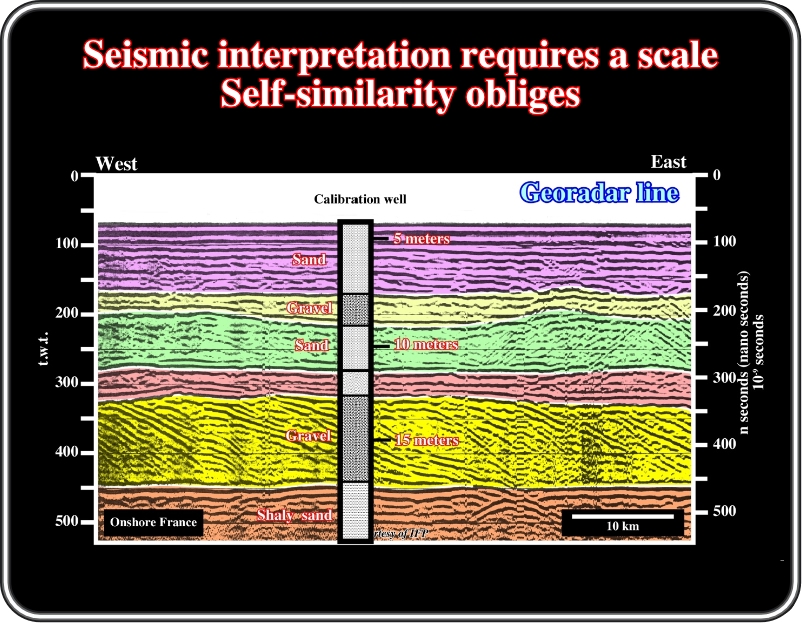
This line is a georadar line shot in onshore France (Pin Sec). The vertical scale is in nanoseconds. The interpretation was based in a calibration well, in which georadar velocities range from 0,08 to 0,13 ns. The depositional inclined reflectors are not associated to a deltaic or continental slope, but small oblique bedding planes (probably strandlines).

to continue press next